In December 2003, to commemorate the 100th anniversary of the outset flight of the Wright brothers, the New York Times ran a story entitled "Staying Aloft; What Does Keep Them Upwards There?" The point of the slice was a simple question: What keeps planes in the air? To reply it, the Times turned to John D. Anderson, Jr., curator of aerodynamics at the National Air and Space Museum and author of several textbooks in the field.

What Anderson said, yet, is that there is actually no agreement on what generates the aerodynamic strength known as lift. "At that place is no simple one-liner answer to this," he told the Times. People give different answers to the question, some with "religious fervor." More than 15 years after that pronouncement, there are even so different accounts of what generates elevator, each with its own substantial rank of zealous defenders. At this betoken in the history of flight, this situation is slightly puzzling. After all, the natural processes of evolution, working mindlessly, at random and without any understanding of physics, solved the mechanical problem of aerodynamic elevator for soaring birds eons ago. Why should it exist so hard for scientists to explicate what keeps birds, and airliners, up in the air?

Adding to the confusion is the fact that accounts of lift exist on two separate levels of abstraction: the technical and the nontechnical. They are complementary rather than contradictory, just they differ in their aims. I exists every bit a strictly mathematical theory, a realm in which the analysis medium consists of equations, symbols, computer simulations and numbers. There is little, if whatsoever, serious disagreement equally to what the appropriate equations or their solutions are. The objective of technical mathematical theory is to make accurate predictions and to projection results that are useful to aeronautical engineers engaged in the circuitous business organisation of designing aircraft.

But by themselves, equations are not explanations, and neither are their solutions. There is a second, nontechnical level of analysis that is intended to provide u.s.a. with a physical, commonsense explanation of lift. The objective of the nontechnical approach is to requite us an intuitive understanding of the actual forces and factors that are at work in belongings an plane aloft. This arroyo exists not on the level of numbers and equations but rather on the level of concepts and principles that are familiar and intelligible to nonspecialists.

It is on this second, nontechnical level where the controversies lie. Two different theories are commonly proposed to explain lift, and advocates on both sides argue their viewpoints in articles, in books and online. The problem is that each of these 2 nontechnical theories is correct in itself. Simply neither produces a complete explanation of lift, i that provides a full accounting of all the basic forces, factors and physical conditions governing aerodynamic elevator, with no issues left dangling, unexplained or unknown. Does such a theory even exist?

Two Competing Theories

By far the almost pop caption of lift is Bernoulli's theorem, a principle identified by Swiss mathematician Daniel Bernoulli in his 1738 treatise, Hydrodynamica. Bernoulli came from a family of mathematicians. His father, Johann, made contributions to the calculus, and his Uncle Jakob coined the term "integral." Many of Daniel Bernoulli's contributions had to do with fluid flow: Air is a fluid, and the theorem associated with his name is commonly expressed in terms of fluid dynamics. Stated just, Bernoulli's constabulary says that the force per unit area of a fluid decreases as its velocity increases, and vice versa.

Bernoulli's theorem attempts to explicate elevator as a consequence of the curved upper surface of an airfoil, the technical name for an aeroplane wing. Considering of this curvature, the idea goes, air traveling across the top of the wing moves faster than the air moving along the wing's bottom surface, which is apartment. Bernoulli'southward theorem says that the increased speed atop the fly is associated with a region of lower pressure level there, which is elevator.

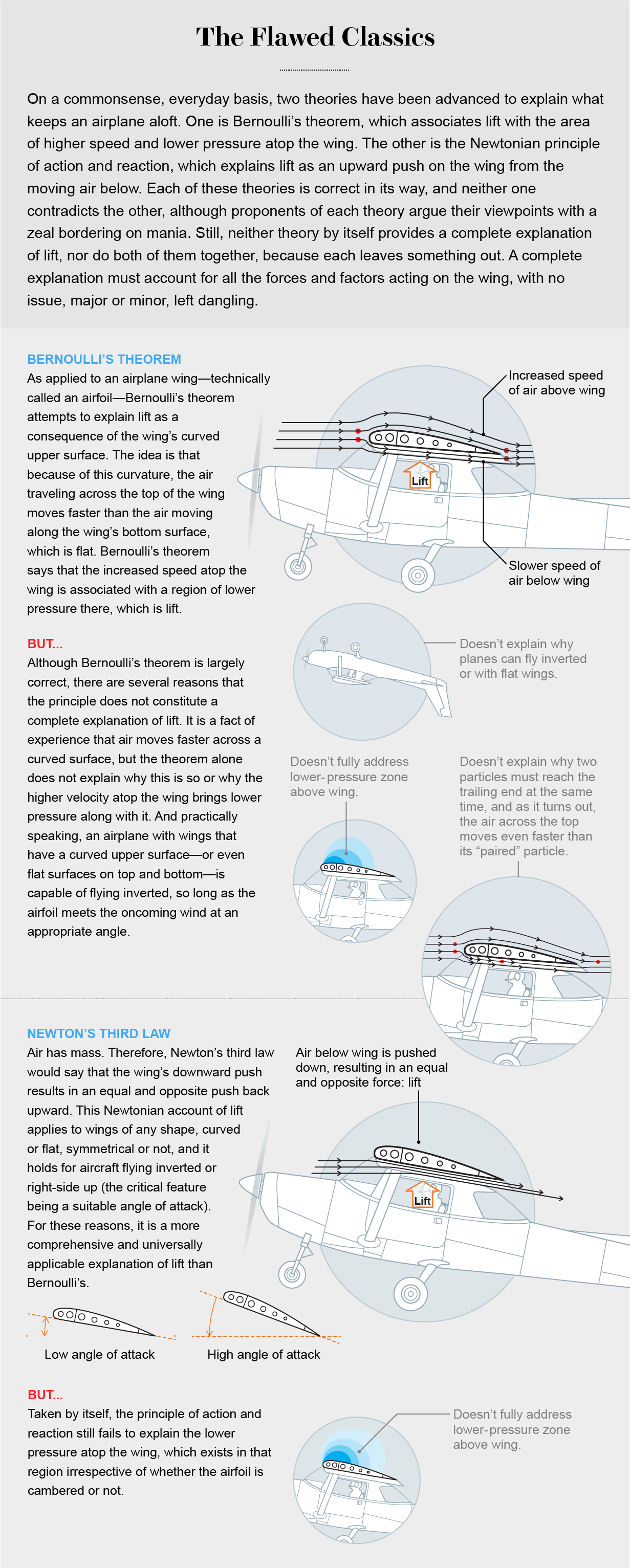
Illustration depicts two classic explanations of lift—Bernoulli's theorem and the Newtonian principle of action and reaction—along with their flaws
Credit: L-Dopa

Mountains of empirical information from streamlines (lines of fume particles) in wind-tunnel tests, laboratory experiments on nozzles and Venturi tubes, and and so on provide overwhelming evidence that as stated, Bernoulli's principle is correct and truthful. Even so, in that location are several reasons that Bernoulli's theorem does non by itself found a complete explanation of lift. Although it is a fact of feel that air moves faster across a curved surface, Bernoulli'south theorem alone does not explain why this is so. In other words, the theorem does not say how the college velocity to a higher place the wing came about to begin with.

Art depicts two recent attempts at more complete explanations of lift: co-dependency of lift's four elements, and the cause of low pressure above the wing
Credit: L-Dopa

In that location are enough of bad explanations for the higher velocity. According to the about common one—the "equal transit time" theory—parcels of air that carve up at the wing'southward leading border must rejoin simultaneously at the trailing edge. Considering the top parcel travels further than the lower parcel in a given amount of time, it must go faster. The fallacy here is that there is no physical reason that the two parcels must reach the trailing edge simultaneously. And indeed, they do non: the empirical fact is that the air atop moves much faster than the equal transit fourth dimension theory could account for.

There is also a notorious "sit-in" of Bernoulli's principle, one that is repeated in many popular accounts, YouTube videos and even some textbooks. Information technology involves holding a sheet of paper horizontally at your mouth and blowing across the curved pinnacle of information technology. The page rises, supposedly illustrating the Bernoulli outcome. The reverse result ought to occur when you blow across the lesser of the sheet: the velocity of the moving air below it should pull the page downward. Instead, paradoxically, the page rises.

The lifting of the curved newspaper when menses is applied to one side "is not considering air is moving at dissimilar speeds on the ii sides," says Holger Babinsky, a professor of aerodynamics at the University of Cambridge, in his article "How Exercise Wings Work?" To demonstrate this, blow across a direct slice of newspaper—for example, one held so that information technology hangs downward vertically—and witness that the paper does non motion one way or the other, because "the pressure on both sides of the paper is the same, despite the obvious difference in velocity."

The 2d shortcoming of Bernoulli'south theorem is that it does not say how or why the higher velocity atop the wing brings lower pressure level, rather than higher pressure, forth with it. It might exist natural to recall that when a fly'southward curvature displaces air upward, that air is compressed, resulting in increased pressure atop the fly. This kind of "clogging" typically slows things down in ordinary life rather than speeding them up. On a highway, when two or more lanes of traffic merge into i, the cars involved do not become faster; at that place is instead a mass slowdown and peradventure even a traffic jam. Air molecules flowing atop a wing exercise non behave like that, but Bernoulli'due south theorem does non say why not.

The third problem provides the well-nigh decisive statement against regarding Bernoulli's theorem as a complete business relationship of lift: An plane with a curved upper surface is capable of flight inverted. In inverted flight, the curved wing surface becomes the bottom surface, and co-ordinate to Bernoulli'due south theorem, it and then generates reduced pressure level below the wing. That lower force per unit area, added to the force of gravity, should accept the overall effect of pulling the aeroplane downwardly rather than holding it upward. Moreover, aircraft with symmetrical airfoils, with equal curvature on the top and bottom—or even with apartment top and bottom surfaces—are also capable of flying inverted, so long as the airfoil meets the oncoming wind at an appropriate angle of assault. This means that Bernoulli'south theorem alone is bereft to explain these facts.

The other theory of lift is based on Newton'southward tertiary law of motion, the principle of action and reaction. The theory states that a wing keeps an plane up by pushing the air down. Air has mass, and from Newton's third law it follows that the wing'southward down push results in an equal and opposite button dorsum upwardly, which is elevator. The Newtonian account applies to wings of any shape, curved or flat, symmetrical or non. It holds for shipping flying inverted or right-side up. The forces at piece of work are as well familiar from ordinary feel—for case, when yous stick your hand out of a moving car and tilt it up, the air is deflected downward, and your mitt rises. For these reasons, Newton's 3rd law is a more universal and comprehensive explanation of lift than Bernoulli's theorem.

Just taken past itself, the principle of activeness and reaction also fails to explain the lower pressure atop the fly, which exists in that region irrespective of whether the airfoil is cambered. It is only when an airplane lands and comes to a halt that the region of lower force per unit area atop the wing disappears, returns to ambience pressure, and becomes the aforementioned at both acme and bottom. But as long as a airplane is flying, that region of lower pressure is an inescapable element of aerodynamic lift, and it must be explained.

Historical Agreement

Neither Bernoulli nor Newton was consciously trying to explain what holds shipping up, of course, because they lived long earlier the bodily development of mechanical flying. Their respective laws and theories were just repurposed once the Wright brothers flew, making it a serious and pressing business for scientists to empathise aerodynamic lift.

Most of these theoretical accounts came from Europe. In the early years of the 20th century, several British scientists advanced technical, mathematical accounts of lift that treated air as a perfect fluid, meaning that it was incompressible and had zero viscosity. These were unrealistic assumptions but perhaps understandable ones for scientists faced with the new phenomenon of controlled, powered mechanical flying. These assumptions also made the underlying mathematics simpler and more than straightforward than they otherwise would have been, merely that simplicity came at a price: all the same successful the accounts of airfoils moving in platonic gases might be mathematically, they remained defective empirically.

In Germany, one of the scientists who applied themselves to the problem of lift was none other than Albert Einstein. In 1916 Einstein published a brusk slice in the periodical Die Naturwissenschaften entitled "Simple Theory of Water Waves and of Flying," which sought to explain what accounted for the carrying capacity of the wings of flying machines and soaring birds. "In that location is a lot of obscurity surrounding these questions," Einstein wrote. "Indeed, I must confess that I have never encountered a elementary answer to them fifty-fifty in the specialist literature."

Einstein then proceeded to give an explanation that assumed an incompressible, frictionless fluid—that is, an platonic fluid. Without mentioning Bernoulli by proper noun, he gave an account that is consistent with Bernoulli'south principle by saying that fluid pressure is greater where its velocity is slower, and vice versa. To take advantage of these pressure differences, Einstein proposed an airfoil with a burl on top such that the shape would increase airflow velocity above the bulge and thus decrease pressure there also.

Einstein probably idea that his ideal-fluid analysis would apply equally well to existent-world fluid flows. In 1917, on the basis of his theory, Einstein designed an airfoil that later came to be known as a true cat'due south-dorsum wing because of its resemblance to the humped back of a stretching cat. He brought the design to aircraft manufacturer LVG (Luftverkehrsgesellschaft) in Berlin, which built a new flying machine effectually it. A test pilot reported that the craft waddled around in the air like "a pregnant duck." Much afterwards, in 1954, Einstein himself called his circuit into aeronautics a "youthful folly." The individual who gave us radically new theories that penetrated both the smallest and the largest components of the universe nonetheless failed to brand a positive contribution to the understanding of lift or to come upwardly with a practical airfoil design.

Toward a Complete Theory of Lift

Contemporary scientific approaches to aircraft pattern are the province of computational fluid dynamics (CFD) simulations and the so-called Navier-Stokes equations, which take full account of the actual viscosity of existent air. The solutions of those equations and the output of the CFD simulations yield force per unit area-distribution predictions, airflow patterns and quantitative results that are the basis for today's highly avant-garde aircraft designs. Still, they exercise not by themselves requite a physical, qualitative caption of lift.

In recent years, however, leading aerodynamicist Doug McLean has attempted to go beyond sheer mathematical ceremonial and come to grips with the physical crusade-and-effect relations that account for lift in all of its existent-life manifestations. McLean, who spent most of his professional career as an engineer at Boeing Commercial Airplanes, where he specialized in CFD code development, published his new ideas in the 2012 text Understanding Aerodynamics: Arguing from the Existent Physics.

Considering that the volume runs to more than 500 pages of fairly dense technical analysis, it is surprising to see that it includes a section (seven.iii.3) entitled "A Bones Caption of Elevator on an Airfoil, Attainable to a Nontechnical Audience." Producing these xvi pages was not easy for McLean, a principal of the bailiwick; indeed, it was "probably the hardest part of the volume to write," the author says. "Information technology saw more than revisions than I tin can count. I was never entirely happy with it."

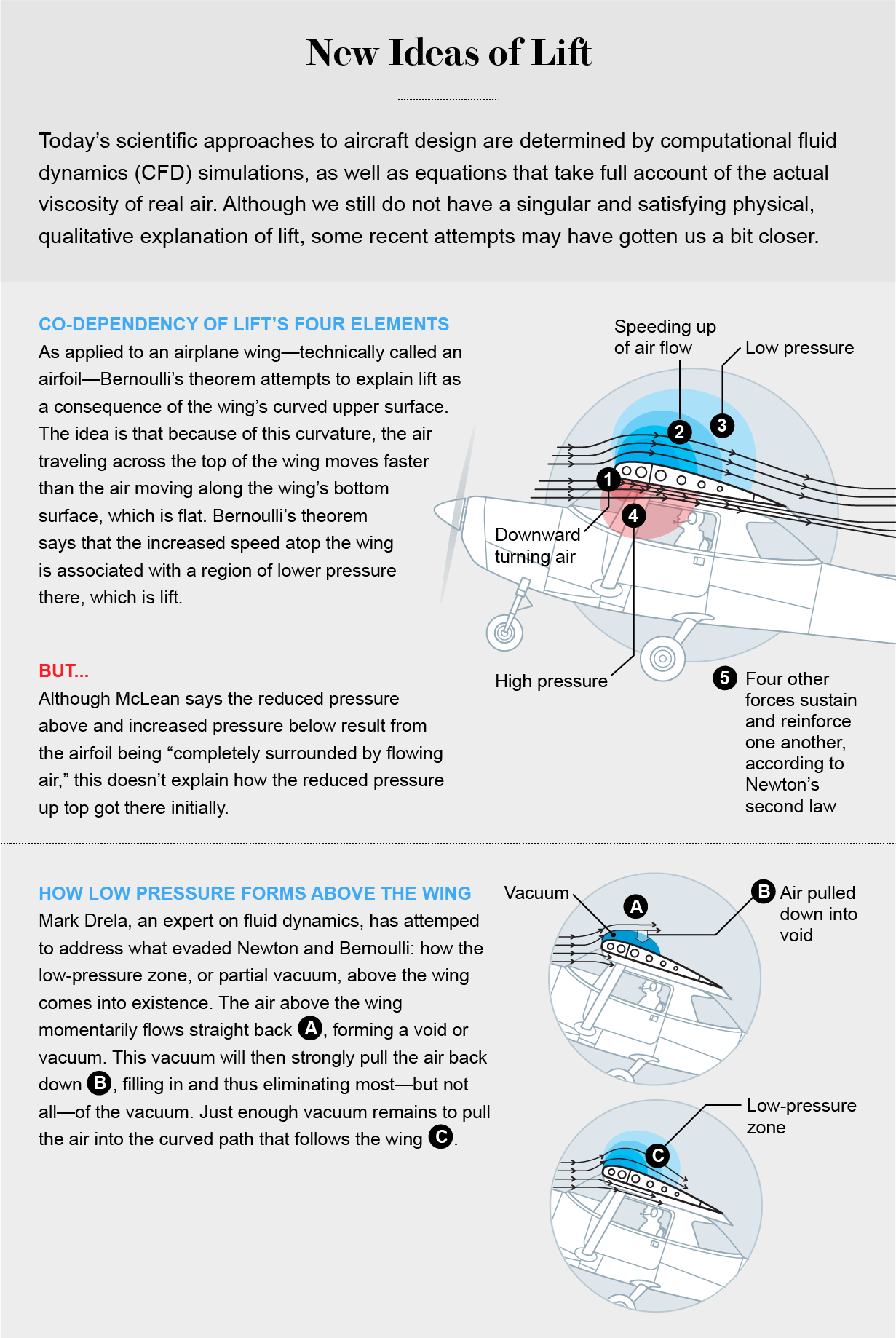
McLean's complex explanation of lift starts with the bones assumption of all ordinary aerodynamics: the air effectually a fly acts as "a continuous material that deforms to follow the contours of the airfoil." That deformation exists in the form of a deep swath of fluid flow both above and beneath the wing. "The airfoil affects the pressure over a wide expanse in what is called a pressure field," McLean writes. "When lift is produced, a lengthened cloud of depression pressure level always forms above the airfoil, and a diffuse cloud of loftier pressure usually forms below. Where these clouds bear upon the airfoil they plant the pressure difference that exerts lift on the airfoil."

Water-channel test at NASA Ames Fluid Mechanics Labuses fluorescent dye to visualize the catamenia field over an airplane wing. The streamlines, moving from left to right and curving as they encounter the wing, help to illustrate the physics of lift. Credit: Ian Allen

The wing pushes the air downwards, resulting in a downward plough of the airflow. The air to a higher place the fly is sped up in accordance with Bernoulli's principle. In addition, there is an expanse of high force per unit area below the wing and a region of low pressure above. This means that at that place are four necessary components in McLean'southward explanation of lift: a downward turning of the airflow, an increment in the airflow's speed, an surface area of depression pressure level and an surface area of high pressure.

But it is the interrelation among these four elements that is the nigh novel and distinctive attribute of McLean's account. "They support each other in a reciprocal cause-and-effect human relationship, and none would exist without the others," he writes. "The pressure differences exert the lift force on the airfoil, while the downward turning of the flow and the changes in flow speed sustain the pressure level differences." It is this interrelation that constitutes a fifth element of McLean's explanation: the reciprocity among the other four. Information technology is every bit if those four components collectively bring themselves into existence, and sustain themselves, by simultaneous acts of common creation and causation.

There seems to be a hint of magic in this synergy. The process that McLean describes seems alike to four agile agents pulling up on one another'south bootstraps to continue themselves in the air collectively. Or, every bit he acknowledges, it is a case of "circular cause-and-result." How is it possible for each element of the interaction to sustain and reinforce all of the others? And what causes this mutual, reciprocal, dynamic interaction? McLean's respond: Newton'southward second law of motion.

Newton's second law states that the acceleration of a body, or a package of fluid, is proportional to the force exerted on information technology. "Newton's second law tells us that when a pressure difference imposes a cyberspace forcefulness on a fluid parcel, it must crusade a alter in the speed or direction (or both) of the bundle's motion," McLean explains. Just reciprocally, the force per unit area difference depends on and exists because of the parcel'southward dispatch.

Aren't we getting something for zippo here? McLean says no: If the wing were at residue, no office of this cluster of mutually reinforcing activity would exist. But the fact that the wing is moving through the air, with each parcel affecting all of the others, brings these co-dependent elements into existence and sustains them throughout the flight.

Turning on the Reciprocity of Lift

Soon subsequently the publication of Understanding Aerodynamics, McLean realized that he had non fully accounted for all the elements of aerodynamic lift, because he did not explain convincingly what causes the pressures on the fly to change from ambient. Then, in November 2018, McLean published a two-role commodity in The Physics Instructor in which he proposed "a comprehensive concrete explanation" of aerodynamic lift.

Although the commodity largely restates McLean'southward earlier line of statement, information technology besides attempts to add a better explanation of what causes the pressure level field to be nonuniform and to assume the physical shape that information technology does. In particular, his new argument introduces a mutual interaction at the menstruation field level and then that the nonuniform pressure field is a issue of an applied forcefulness, the downward force exerted on the air by the airfoil.

Whether McLean's department seven.3.iii and his follow-up article are successful in providing a complete and correct account of lift is open up to interpretation and debate. There are reasons that it is difficult to produce a clear, simple and satisfactory account of aerodynamic elevator. For one thing, fluid flows are more than complex and harder to sympathise than the motions of solid objects, especially fluid flows that separate at the fly'south leading edge and are subject to different physical forces forth the superlative and bottom. Some of the disputes regarding elevator involve not the facts themselves merely rather how those facts are to exist interpreted, which may involve problems that are incommunicable to make up one's mind past experiment.

Still, there are at this indicate only a few outstanding matters that crave explanation. Lift, every bit you lot will recall, is the upshot of the force per unit area differences between the top and bottom parts of an airfoil. We already have an acceptable explanation for what happens at the bottom part of an airfoil: the oncoming air pushes on the wing both vertically (producing lift) and horizontally (producing elevate). The upwards push exists in the form of higher pressure beneath the wing, and this higher pressure level is a event of simple Newtonian action and reaction.

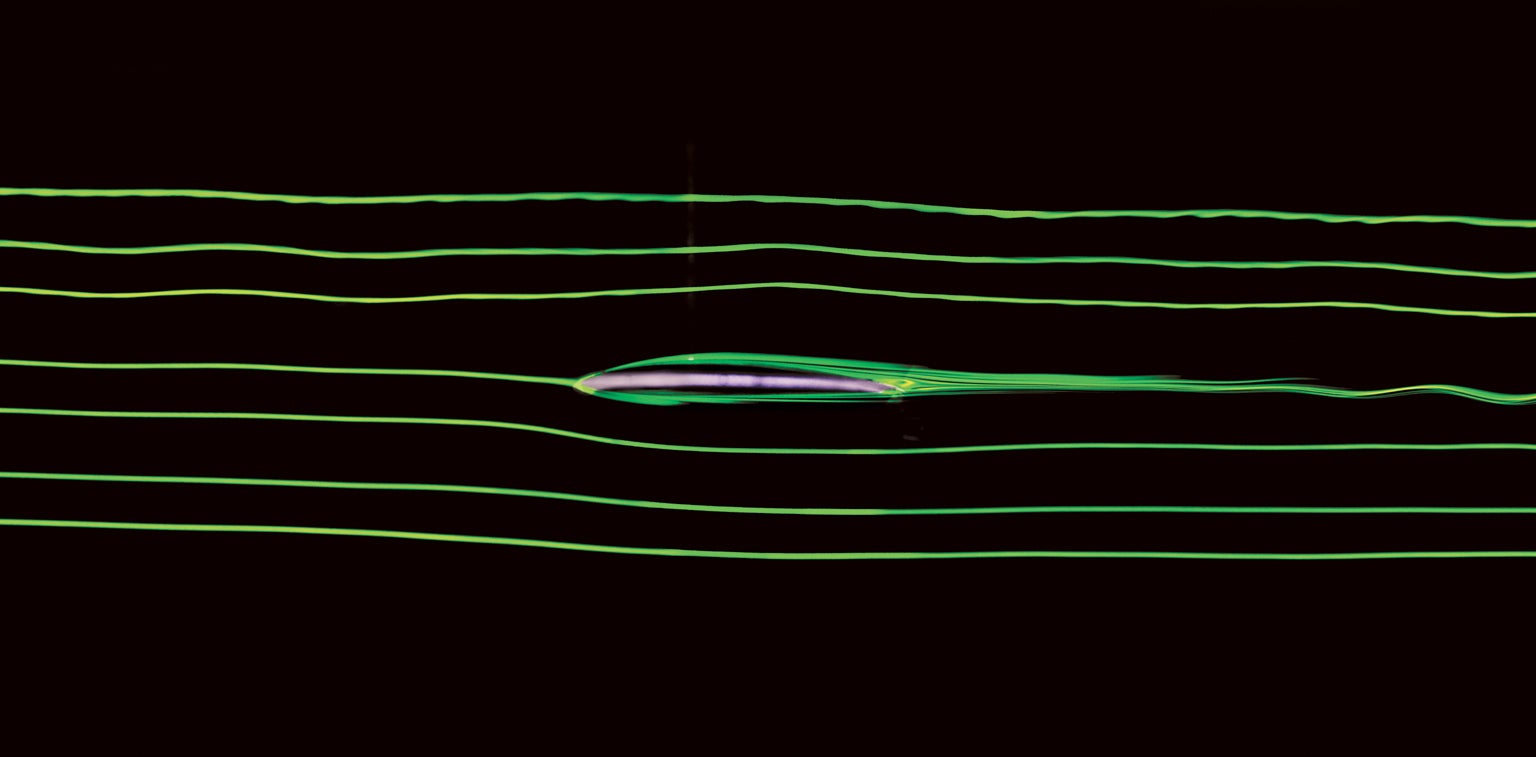
Things are quite different at the acme of the wing, however. A region of lower pressure level exists there that is also function of the aerodynamic lifting force. Only if neither Bernoulli's principle nor Newton's tertiary law explains it, what does? We know from streamlines that the air above the wing adheres closely to the downwardly curvature of the airfoil. But why must the parcels of air moving across the wing's top surface follow its downward curvature? Why tin can't they carve up from it and fly straight dorsum?

Mark Drela, a professor of fluid dynamics at the Massachusetts Constitute of Technology and author of Flying Vehicle Aerodynamics, offers an answer: "If the parcels momentarily flew off tangent to the airfoil elevation surface, there would literally be a vacuum created below them," he explains. "This vacuum would and then suck down the parcels until they mostly fill in the vacuum, i.due east., until they move tangent to the airfoil once more. This is the concrete mechanism which forces the parcels to move along the airfoil shape. A slight partial vacuum remains to maintain the parcels in a curved path."

This cartoon away or pulling downward of those air parcels from their neighboring parcels in a higher place is what creates the area of lower pressure atop the wing. But another effect as well accompanies this action: the higher airflow speed atop the wing. "The reduced pressure over a lifting wing besides 'pulls horizontally' on air parcels as they approach from upstream, so they take a higher speed by the time they arrive above the wing," Drela says. "Then the increased speed above the lifting fly tin be viewed as a side consequence of the reduced pressure level there."

Simply equally ever, when it comes to explaining lift on a nontechnical level, another expert will accept another answer. Cambridge aerodynamicist Babinsky says, "I detest to disagree with my esteemed colleague Mark Drela, only if the creation of a vacuum were the explanation, then it is hard to explain why sometimes the menstruum does nevertheless separate from the surface. Only he is correct in everything else. The problem is that at that place is no quick and piece of cake explanation."

Drela himself concedes that his explanation is unsatisfactory in some ways. "1 apparent problem is that there is no explanation that volition be universally accepted," he says. And so where does that leave us? In effect, right where nosotros started: with John D. Anderson, who stated, "In that location is no simple 1-liner answer to this."